Question

Assume the height of the parabola at the base of the Eiffel Tower is 75 meters, and the inside width is 124 meters. Using the picture below (in the first quadrant of the rectangular coordinate system), please answer the following questions.

What is the vertex of the parabola?

What is the domain and range of the parabola that develops the base of the Eiffel Tower?

What are the x-intercepts

Find the equation in standard form that represents the parabola?

Answer 1

Vertex = (0,75)

Domain in interval notation is (-62,62)

Range in interval notation is (0,75).

The x-intercepts are (-62,0) and (62,0)

The equation of the parabola in standard form is

`y = - (75)/(3844) {x}^(2) + 75`

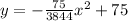
How the equation of the parabola is determined.

From the given information

vertex of the parabola equivalent to coordinate of the height.

vertex = (0, 75)

The width = 124

x = 124/2 = +-62

The x-intercepts are (-62, 0) and (62,0)

The domain is all values of x that define the parabola

that's (-62,62)

The range is all output values of the function. The y- values from 0 to 75.

The standard form of parabolic equation is

y = a(x - h)² + k

To find the coefficient of square value a, set h and y to 0

0 = a(62 - 0)² + 75

y = 0, h = 0, k = 75 and x = 62

0 = 3844a + 75

3844a = -75

a = -75/3844

Write the equation

y = a(x - h)² + k

y = -75/3844(x - 0)² + k

y = -75/3844(x²) + 75

`y = - (75)/(3844) {x}^(2) + 75`

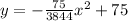
This is the equation of the parabola