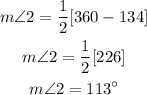Question

Find the measure of the arcindicated.or angle1. m1 =2. m 2 =S6ySR134°146

Answer 1

From the first figure

Since LR and JV are 2 chords intersected at a point inside the circle, then

`180-m\angle1=(1)/(2)\lbrack56+146\rbrack`

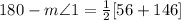
The angle next to <1 and form a line JV with it

`\begin{gathered} 180-m\angle1=(1)/(2)\lbrack202\rbrack \\ 180-m\angle1=101 \end{gathered}`

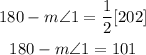
Add m<1 to both sides and subtract 101 from both sides

`\begin{gathered} 180-m\angle1+m\angle1-101=101-101+m\angle1 \\ 79^(\circ)=m\angle1 \end{gathered}`

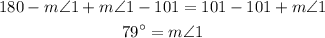
In the second figure

Since TU is a tangent to the circle at point T

Since ST is a chord in the circle

Then angle of tangency subtended by the major arc ST, Its measure is half the measure of the subtended arc.

Since the major arc ST = the measure of the circle - the measure of the minor arc ST

`m\angle2=(1)/(2)\lbrack360-arcST\rbrack`

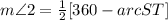
Since the measure of the minor arc ST is 134 degrees, then

`\begin{gathered} m\angle2=(1)/(2)\lbrack360-134\rbrack \\ m\angle2=(1)/(2)\lbrack226\rbrack \\ m\angle2=113^(\circ) \end{gathered}`