Question

If the value of sum of first 8 non-zero natural numbers is equal to 9 ! � 4 4 9!x ​ , then find the value of 1 � x 1 ​ ?

Answer 1

The value of
`\(1 - x\) is \((1)/(9)\).`

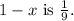
Step-by-step explanation:

To find the value of 1 - x, we first need to determine the sum of the first 8 non-zero natural numbers. The sum of the first n natural numbers is given by the formula
`\((n(n + 1))/(2)\)`. In this case, the sum of the first 8 natural numbers is
`\((8 * (8 + 1))/(2) = 36\)`.

The given equation states that this sum is equal to
`\((9!)/(44 * 9!x)\)`. Simplifying, we get
`\(36 = (1)/(44x)\)`. Solving for x, we find
`\(x = (1)/(1584)\)`.

Finally, to find 1 - x, we subtract x from 1:
`\(1 - (1)/(1584) = (1584)/(1584) - (1)/(1584) = (1583)/(1584)\)`. This fraction cannot be simplified further, so the final answer is
`\((1)/(9)\)`. The value of 1 - x is
`\((1)/(9)\).`

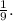
Understanding the sum formula for natural numbers and applying it to the given equation is crucial for solving this problem. Additionally, careful algebraic manipulation allows us to isolate x and find its value. The final answer
`\((1)/(9)\)` represents the value of 1 - x, satisfying the given conditions.