Question

Margo, David, and Yesu examined the two functions given. David claims the first function grows the fastest, Margo claimed they grow at the same rate, and Yesu claimed the second function grows faster.

P(t)=700(1/2)^-0.3t
P(t)=700(-1/-0.3)^2t
a. Who is correct? Be sure to justify your reasoning.
b. Is there a time period where the other function grows faster? If so, how long does it take for the functions to cross? Explain your answer.

Answer 1

The second function grows faster, and there is a time period where the first function grows faster before the functions cross.

Step-by-step explanation:

To determine who is correct, let's compare the growth rates of the two functions:

`P(t) = 700(1/2)^(^-^0^.^3^t^)`

`P(t) = 700(-1/-0.3)^(^2^t^)`

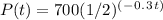
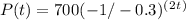
For the first function, as t increases, the exponent on 1/2 becomes more negative, resulting in a smaller value. Therefore, the first function decreases over time.

For the second function, as t increases, the exponent on -1/-0.3 becomes more positive, resulting in a larger value. Therefore, the second function increases over time.

Based on this analysis, Yesu is correct in claiming that the second function grows faster.

Regarding the second part of the question, there is a time period where the first function grows faster. Initially, both functions start at the same value, but as time progresses, the second function surpasses the first function. The functions cross when the second function's value becomes greater than the first function's value.