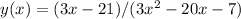
Final answer:
To determine the domain and range of the function y(x) = (3x - 21) / (3x^2 - 20x - 7), we must factor, find the points of discontinuity, and identify asymptotes. The domain excludes x = -1/3 and x = 7. The range includes all real numbers.
Step-by-step explanation:
Steps to Find the Domain and Range of the Rational Function
To find the domain and range of the given rational function
we will perform the following steps:
- Factor the numerator and denominator: The numerator can be factored as 3(x - 7). Factoring the denominator will require finding two numbers that multiply to give -21 (since 3*(-7)=-21) and add to give -20, resulting in (3x + 1)(x - 7).
- Determine the point of discontinuity if it exists: The points of discontinuity are where the denominator equals zero. Set the denominator equal to zero and solve for x, which gives us x = -1/3 and x = 7.
- Determine vertical asymptote: The vertical asymptotes are x = -1/3 and x = 7, where the denominator is zero and the function is undefined.
- Determine horizontal asymptote: Since the highest power of the terms in the numerator and denominator are the same, the horizontal asymptote is the ratio of the leading coefficients, which is y = 0.
- Describe the domain in a complete sentence: The domain of the function is all real numbers except x = -1/3 and x = 7.
- Write domain in set notation: The domain in set notation is x ≠ -1/3, x ≠ 7.
- Write domain in inequality notation: The domain in inequality notation is x ≠ -1/3 and x ≠ 7.
- Write domain in interval notation: The domain in interval notation is (-∞, -1/3) ∪ (-1/3, 7) ∪ (7, +∞).
- Describe the range in a complete sentence: The range of the function is all real numbers because there is no restriction on the possible values of y.
- Write range in set notation: The range in set notation is {y ∈ ℝ}.
- Write range in inequality notation: The range in inequality notation is -∞ < y < +∞.
- Write range in interval notation: The range in interval notation is (-∞, +∞).