Question

May you write a equation of a line that is perpendicular to, " y = 1/3x + 3" and passes through (-1, -2)?

Answer 1

the general equation of a graph is y= mx + c

m is the gradient and c is the intercept

from the first line equation, m = 1/3

condition for perpendicularity is that if two lines are perpendicular

the gradient of the first line is equal to the negative of the reciprocal of the second line gradient

so

`\begin{gathered} \text{if m}_{1\text{ }}is\text{ the gradient of the first line and } \\ m_{2\text{ }}is\text{ the gradient of the second line} \end{gathered}`
`(-1)/(m_2)=m_1`
`\begin{gathered} m_1=\text{ }(1)/(3),\text{ then } \\ m_2=\text{ -}((1)/(1))/(3)\text{ =- }(1)/(1)*(3)/(1)=-3 \end{gathered}`
`\begin{gathered} \text{if it passes through the points (-1,-2)} \\ x\text{ = -1, y=-2} \\ \text{use y= mx +c to obtain the value of c by substituting m, x and y} \end{gathered}`
`\begin{gathered} y=mx\text{ + c} \\ -2\text{ = -3 }*-1\text{ +c} \\ -2\text{ = 3 + c} \\ -2-3\text{ =c} \\ -5\text{ =c} \\ c=\text{ -5} \end{gathered}`

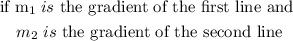
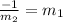
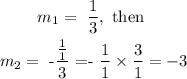
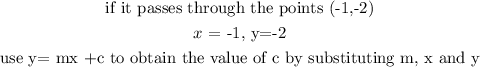
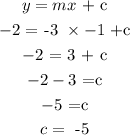
so the equation of the line is obtain by substituting the values of the gradient (m2) and the intercept (c) in y = mx +c

so the equation is y = -3x + (-5)

y = -3x -5