The length and width of a rectangle must have a sum of 36 feet.
Let the length of the rectangle is L and the width of the rectangle is W
Since it is given that, the length and width of a rectangle must have a sum of 36 feet.
i.e.,
L + W = 36 .......(i)
Area of rectangle is defined as the product of the length with width
i.e.,
Area of Rectangle = Length x Width
A = L x W .........(ii)
From the equation (i)
L + W = 36
W = 36 - L
SUbstitute the value of W = 36-L in the equation (i)
A = L x W
A = L x (36-L)
A = 36L - L²
Differentiate the area with respect to L
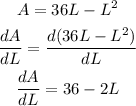
Equate dA/dL = 0
36-2L = 0
2L = 36
L = 18
Substitute the value of L = 18 in the equation (i);
L + W = 36
18 + W = 36
W = 36 - 18
W = 18
Again differentiate the equation dA/dL
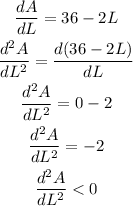
Thus, area is maximum or as large as possible
Answer : Dimension of rectangle;
Length = 18 feet
Width = 18 feet
....