Question

The length and width of a rectangle must have a sum of 36 feet. Find the dimensions of the rectangle whose area is as large as possible.

Answer 1

The length and width of a rectangle must have a sum of 36 feet.

Let the length of the rectangle is L and the width of the rectangle is W

Since it is given that, the length and width of a rectangle must have a sum of 36 feet.

i.e.,

L + W = 36 .......(i)

Area of rectangle is defined as the product of the length with width

i.e.,

Area of Rectangle = Length x Width

A = L x W .........(ii)

From the equation (i)

L + W = 36

W = 36 - L

SUbstitute the value of W = 36-L in the equation (i)

A = L x W

A = L x (36-L)

A = 36L - L²

Differentiate the area with respect to L

`\begin{gathered} A=36L-L^2 \\ (dA)/(dL)=(d(36L-L^2))/(dL) \\ (dA)/(dL)=36-2L \end{gathered}`

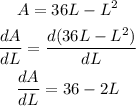
Equate dA/dL = 0

36-2L = 0

2L = 36

L = 18

Substitute the value of L = 18 in the equation (i);

L + W = 36

18 + W = 36

W = 36 - 18

W = 18

Again differentiate the equation dA/dL

`\begin{gathered} (dA)/(dL)=36-2L \\ (d^2A)/(dL^2)=(d(36-2L))/(dL) \\ (d^2A)/(dL^2)=0-2 \\ (d^2A)/(dL^2)=-2 \\ (d^2A)/(dL^2)<0 \end{gathered}`

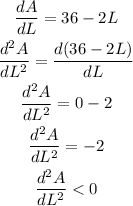
Thus, area is maximum or as large as possible

Answer : Dimension of rectangle;

Length = 18 feet

Width = 18 feet

....