Question

Which characteristic is correct for the function f(x)=−6x5+4x3? neither even nor oddoddevenboth even and odd

Answer 1

The given function is:

`f(x)=-6x^5+4x^3`

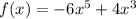
Even functions are unchanged when reflected over the y-axis, so:

`f(-x)=f(x)`

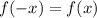
Odd functions are unchanged when rotated 180° about the origin, so:

`f(-x)=-f(x)`

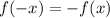
Now, replace -x as the argument of the function and let's observe the result:

`\begin{gathered} f(-x)=-6(-x)^5+4(-x)^3 \\ f(-x)=-6*-x^5+4*-x^3 \\ f(-x)=6x^5-4x^3 \end{gathered}`

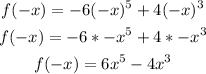
As can be observed, f(-x) is not equal to f(x), then this is not an even function.

Now, let's evaluate -f(x):

`\begin{gathered} -f(x)=-(-6x^5+4x^3) \\ -f(x)=-(-6x^5)-(4x^3) \\ -f(x)=6x^5-4x^3 \\ THEN \\ f(-x)=-f(x) \end{gathered}`

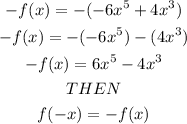
This function is odd.