Answer:
- Approximately
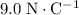 at
at
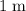 from this charge, pointing away from the point charge.
from this charge, pointing away from the point charge. - Approximately
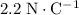 at
at
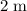 from this charge, pointing away from the point charge.
from this charge, pointing away from the point charge. - Approximately
 at
at
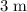 from this charge, pointing away from the point charge.
from this charge, pointing away from the point charge.
Assumption: there is no object between this point charge and the observer.
Step-by-step explanation:
The electric field of a point charge is inversely proportional to the square of the distance from that point charge.
Let
 denote Coulomb's constant (
denote Coulomb's constant (
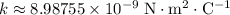 .) Let the magnitude of that point charge be
.) Let the magnitude of that point charge be
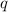 . At a distance of
. At a distance of
 from this charge, the electric field due to this charge would be:
from this charge, the electric field due to this charge would be:
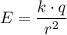 .
.
Convert the magnitude of the point charge in this question to standard units:
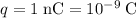 .
.
Apply that equation to find the magnitude of the electric field due to this point charge:
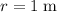 :
:
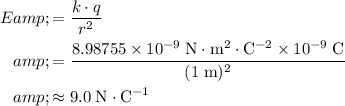 .
.
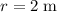 :
:
 .
.
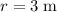 :
:
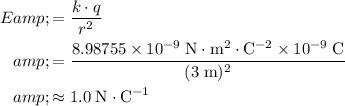 .
.
The direction of the electric field at a point is the same as the direction of a force from this field onto a positive point charge at this point.
Because the
 point charge here is positive, the electric field of this charge would repel other positive point charges. Hence, the electric field around this
point charge here is positive, the electric field of this charge would repel other positive point charges. Hence, the electric field around this
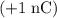 point charge at any point in the field would point away from this charge.
point charge at any point in the field would point away from this charge.