2 Answers

Jefsmi · Answer 1 · 2024-06-08T15:14:54+0000

The equation of a circle with center at the origin and radius 6 is x^2 + y^2 = 36.

The equation of a circle with center at the origin and radius 6 can be written as:

x2 + y2 = r2

Substituting r with 6:

x2 + y2 = 62

Simplifying the equation:

x2 + y2 = 36

Dops · Answer 2 · 2024-06-11T05:51:51+0000

Answer:

$\sf \textsf{Equation of a circle} = x^2 + y^2 = 36$

Step-by-step explanation:

The equation of a circle with center
$\sf (h, k)$ and radius
$\sf r$ is given by the formula:

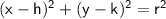
$\sf (x - h)^2 + (y - k)^2 = r^2$

In this case, since the center is at the origin
$\sf (0, 0)$ and the radius is
$\sf 6$ , the equation becomes:

$\sf x^2 + y^2 = 6^2$

Simplifying further:

$\sf x^2 + y^2 = 36$

So, the equation of the circle with center at the origin and radius
$\sf 6$ is
$\sf x^2 + y^2 = 36$ .

Please log in or register to add a comment.