Answer:
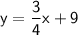
Step-by-step explanation:
To write the equation of a line given a point
 and the slope
and the slope
 , we can use the point-slope form of a linear equation:
, we can use the point-slope form of a linear equation:
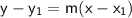
In this case, we have the point
 and the slope
and the slope
 .
.
Substitute these values into the formula:
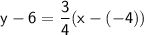
Now, simplify the equation:
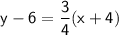
Distribute the
 to both terms inside the parentheses:
to both terms inside the parentheses:
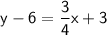
Now, add 6 to both sides of the equation to isolate
 :
:
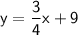
So, the equation of the line with a slope of
 and passing through the point
and passing through the point
 is
is
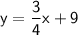 .
.