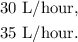Question

The Evans family and the Brown family each used their sprinklers last summer. The Evans family's sprinkler was used for 25 hours. The Brown family's sprinkler was used for 40 hours. There was a combined total output of 2150 L of water. What was the water output rate for each sprinkler if the sum of the two rates was 65 L per hour?

Answer 1

Using the given information, we set the following system of equations:

`\begin{gathered} 25r_1+40r_2=2150, \\ r_1+r_2=65. \end{gathered}`

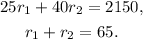
Where r₁, and r₂ are the rates.

Multiplying the second equation by -25, and adding it to the first equation, we get:

`25r_1+40r_2-25r_1-25r_2=2150-1625.`

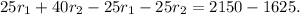
Solving the above equation for r₂, we get:

`\begin{gathered} 15r_2=525, \\ r_2=(525)/(15), \\ r_2=35. \end{gathered}`

Substituting the above value in the second equation, and solving for r₁, we get:

`\begin{gathered} r_1=65-35, \\ r_1=30. \end{gathered}`

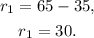
Answer:

`\begin{gathered} 30\text{ L/hour,} \\ 35\text{ L/hour.} \end{gathered}`