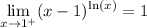Answer:
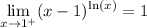
Explanation:
We are given:
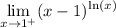
And we want to evaluate it using L'Hopital's Rule.
First, using direct substitution, we will acquire:
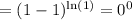
Which is indeterminate.
In order to apply L'Hopital's Rule, we first need to manipulate the expression. We will let:
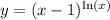
By taking the natural log of both sides:
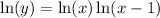
And by taking the limit as x approaches 1 from the right of both functions:
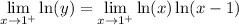
Rewrite:
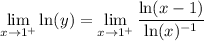
Using direct substitution on the right will result in 0/0. Hence, we can now apply L'Hopital's Rule:
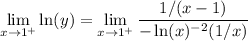
Simplify:
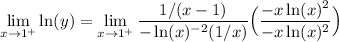
Simplify:
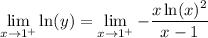
Now, by using direct substitution, we will acquire:
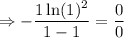
Hence, we will apply L'Hopital's Rule once more. Utilize the product rule:
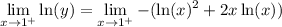
Finally, direct substitution yields:
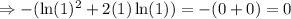
Thus:
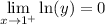
By the Composite Function Property for limits:
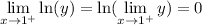
Raising both sides to e produces:
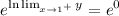
Therefore:
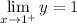
Substitution: