Question

If cos theta = 11 /61 and 270° < theta < 360°, find the exact value of ( sin theta/2 - cos theta/2)²

tysm!!​

Answer 1

By trigonometric expressions and formulae, the exact value of
`\left(\sin 0.5\theta - \cos 0.5\theta\right)^2` is equal to
`(1)/(61)`.

How to determine the exact value of a trigonometric expression

In this problem we need to determine the exact value of a trigonometric expression, this can be done by means of trigonometric functions and trigonometric formulae as well:

Trigonometric formulae required in this question:

`\sin 0.5\theta = \pm \sqrt{(1 - \cos \theta)/(2) }`

`\cos 0.5\theta = \pm \sqrt{(1 + \cos \theta)/(2) }`

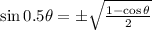
If 270º < θ < 360º, then we need to use the following expressions: (sin 0.5θ < 0, cos 0.5θ > 0)

`\sin 0.5\theta = -\sqrt{(1 - (11)/(61) )/(2) }`

`\sin 0.5\theta = -(5√(61))/(61)`

`\cos 0.5\theta = -\sqrt{(1 + (11)/(61) )/(2) }`

`\cos 0.5\theta = -(6√(61))/(61)`

Thus, the result of the trigonometric is determined by substitution and simplification of the resulting expression:

`\left(\sin 0.5\theta - \cos 0.5\theta\right)^2`

`\left(-(5√(61))/(61) + (6√(61))/(61)\right)^2`

`(1)/(61)`

Therefore, the trigonometric expression
`\left(\sin 0.5\theta - \cos 0.5\theta\right)^2` is equal to
`(1)/(61)`.