1 Answer

Samiul Alam · Answer 1 · 2024-08-01T17:34:24+0000

The stone will take approximately 4 seconds to reach the top of the cliff. Therefore, the correct answer is D.

We may use the equation of motion to determine how long it will take the stone to reach the top of the cliff:

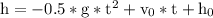
$\rm h = -0.5 * g * t^2 + v_0 * t + h_0$

where

h is the height of the cliff,

g is the acceleration due to gravity (approximately
$\rm 9.8 m/s^2$ ),

t is the time,

$\rm v_0$ is the initial velocity (1 m/s in this case), and

$\rm h_0$ is the initial height of the stone (42 m).

By changing the provided values, we may find the value of t:

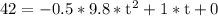
$\rm 42 = -0.5 * 9.8 * t^2 + 1 * t + 0$

$\rm 42 = -4.9 * t^2 + t$

Arranging the equation to the form:

$\rm -4.9 * t^2 + t - 42 = 0$

Using the quadratic formula,

we find that t = 4 seconds or t = -1.7 seconds.

Since time cannot be negative, the stone takes approximately 4 seconds to reach the top of the cliff.

Therefore, the correct answer is D) 4 seconds.

Please log in or register to add a comment.