Answer
a. 1/6
b. 1/30
c. 1/720
d. 1/3
Explanation
a. First, we need to calculate the number of arrangements (like A,B,C,D,E,F; A,C,D,B,F,E, etc.) we can make with six stand-up comics. To calculate this we need to calculate the number of permutations of n = 6 people chosen r = 6 people at a time, as follows:
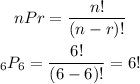
If comic D performs fourth, then we have 5 people (A, B, C, E, and F) and 5 places to order them (1st, 2nd, 3rd, 5th, and 6th). To find the number of ways these arrangements can be made, we need to calculate the number of permutations with n = 5 people chosen r = 5 people at a time, as follows:
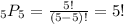
Finally, the probability that Comic D will perform fourth is:

b. If Comic C performs last and Comic B performs fifth, then we need to arrange 4 people in 4 places, that is, we need to calculate the number of permutations with n = 4 people chosen r = 4 people at a time.
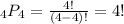
In consequence, the probability that Comic C will perform last and Comic B will perform fifth is:
![\begin{gathered} P(\text{ Comic C will perform last and Comic B will perform fifth})=\frac{number\text{ of ways 4 com}\imaginaryI\text{cs can be ordered}}{number\text{ o fways 6 com}\imaginaryI\text{cs can be ordered}} \\ P(\text{ Comic C will perform last and Comic B will perform fifth})=(4!)/(6!) \\ P(\text{ Comic C will perform last and Comic B will perform fifth})=\frac{4!}{6\cdot5\operatorname{\cdot}4!} \\ P(\text{Com}\imaginaryI\text{c C w}\imaginaryI\text{ll perform last and Com}\imaginaryI\text{c B w}\imaginaryI\text{ll perform f}\imaginaryI\text{fth})=(1)/(30) \end{gathered}]()
c. The order: D, C, B, A, E, F is only one of the total possible arrangements. Then, the probability that the comedians will perform in this order is:
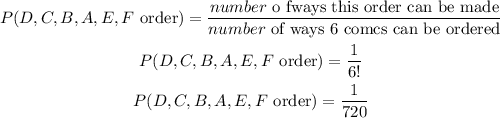
d. The probability that Comic E or Comic F will perform first is computed as follows:
![P(Comic\text{ E will perform first or Comic F will perform first })=P(Comic\text{ E will perform first\rparen+ P\lparen Comic F will perform first\rparen}]()
The probability that Comic E (or F) will perform first is numerically equivalent to the probability that Comic D will perform fourth (which was calculated in item a). Therefore,
