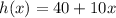Question

The plot below shows the graphs of three functions, f, g, and h, all of which determine the population of three different cities (in thousands of people) in terms of the number of years x since 2000.The population of City A in 2000 was 40 thousand people and the population increased by 13% each year. The function f determines the population of this city (in thousands of people) in terms of x.Write a function formula for f.f(x)=The population of City B in 2000 was 40 thousand people and the population increased by 16% each year. The function g determines the population of this city (in thousands of people) in terms of x.Write a function formula for g.g(x)=The population of City C in 2000 was 40 thousand people and the population increased by 10 thousand people each year. The function h determines the population of this city (in thousands of people) in terms of x.Write a function formula for h.h(x)=

Answer 1

So, here we have an exponential function.

Remember that an exponential function has the form:

`y=a(b)^x=a(1\pm(r)/(100))^x`

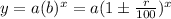
Where a represents an initial amount, and r is the rate of this amount to change. (Increase, or decrease).

So, given that the population of City A in 2000 was 40 thousand people and the population increased by 13% each year, we can say that

`\begin{gathered} a=40 \\ b=1+(13)/(100)=1.13 \end{gathered}`

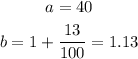
So,

`f(x)=40(1.13)^x`

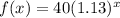
For city B:

`\begin{gathered} a=40 \\ b=1+(16)/(100)=1.16 \\ g(x)=40(1.16)^x \end{gathered}`

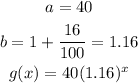
But something different happens with city C. This is not an exponential function, this is a linear function.

So,

`h(x)=40+10x`