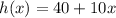So, here we have an exponential function.
Remember that an exponential function has the form:
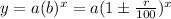
Where a represents an initial amount, and r is the rate of this amount to change. (Increase, or decrease).
So, given that the population of City A in 2000 was 40 thousand people and the population increased by 13% each year, we can say that
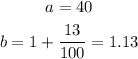
So,
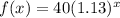
For city B:
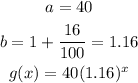
But something different happens with city C. This is not an exponential function, this is a linear function.
So,