Question

-5

-4
-3
-2
- 1
-3
-4
-5
The equation of the line in this graph is y=
2021 Edmentum. All rights reserved.

Answer 1

weThe above question is a linear equation, we can find the equation by doing the following.

1) Determine which type of equation, linear or exponential, will fit the graph.

2) Identify at least three points from the graph.

3) Find the slope of the line, using any two of the points.

4) Find the Y-intercept of the line.

5) Use the slope and Y -intercept to find an equation of the line.

STEP 1

we can identify the following points

`\begin{gathered} x_1=0_{}_{} \\ x_2\text{ = -2} \\ y_1=0_{} \\ y_2\text{ = - 3} \end{gathered}`

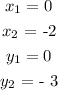
STEP 2

we then find the slope,

`\text{slope(m) = }(y_2-y_1)/(x_2-x_1)\text{ = }(-3-0)/(-2-0)\text{ =}(-3)/(-2)=(3)/(2)`

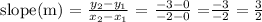
STEP 3

We identify the y-intercept as the point at which the line crosses the y axis.

Y - Intercept(c) = 3

STEP 4

We substitute the value of the slope and the y-intercept into the formula for the equation of a line below.

`y=\text{ mx + c (equation of a line)}`
`\begin{gathered} y\text{ =}(3)/(2)x\text{ + 3} \\ we\text{ multiply through by the lcm of the denominator which is 2} \\ 2\text{ x y = 2 x }(3)/(2)x\text{ + 2 x 3} \\ 2y\text{ = 3x + 6} \end{gathered}`

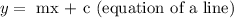
Therefore, the equation of the line in the graph is 2y =3x + 6