Question

Find the critical values of:f(x) = x^3 - 3x^2 + 29

Answer 1

The critical values of a curve f(x) are thepoints in its domain where the derivative f'(x) is zero or not defined.

Given:

It is given that

`f(x)=x^3-3x^2+29`

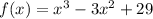
To find critical points first let us find f'(x)

`\begin{gathered} f^(\prime)(x)=(d)/(dx)(x^3-3x^2+29) \\ =3x^2-6x \\ =3x(x-2) \end{gathered}`

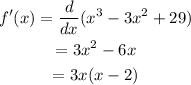
Now on setting f'(x)=0 we have,

`\begin{gathered} 3x(x-2)=0 \\ \Rightarrow3x=0,x-2=0 \\ \Rightarrow x=0,2 \end{gathered}`

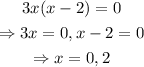
So, the critial values are x=0,2.