Okay, here we have this:
Considering the provided information, we are going to replace in the function f(x)-g(x), with the given values of bounds:
Lower bound (x=4):
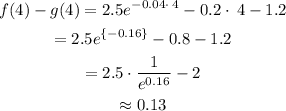
The first value on the right side of the table is the one we just got.
Average of the bounds (x=4.5):
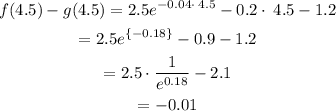
The second value on the right side of the table is the one we just got.
Upper bound:
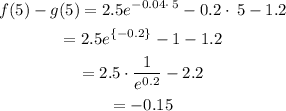
The third value on the right side of the table is the one we just got.