Question

Part CFill in the table, and complete the first iteration of successive approximation using the expression for f(x) - g(x) from partB. Based on where the zero of f(x) – g(x) lies, the starting upper and lower bounds are given.

Answer 1

The above answer was a couple numbers off. Here's the Ed answer.

Answer 2

Okay, here we have this:

Considering the provided information, we are going to replace in the function f(x)-g(x), with the given values of bounds:

Lower bound (x=4):

`\begin{gathered} f(4)-g(4)=2.5e^(-0.04\cdot\: 4)-0.2\cdot\: 4-1.2 \\ =2.5e^{\mleft\{-0.16\mright\}}-0.8-1.2 \\ =2.5\cdot(1)/(e^(0.16))-2 \\ \approx0.13 \end{gathered}`

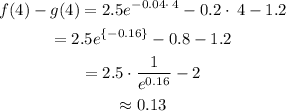
The first value on the right side of the table is the one we just got.

Average of the bounds (x=4.5):

`\begin{gathered} f(4.5)-g(4.5)=2.5e^(-0.04\cdot\: 4.5)-0.2\cdot\: 4.5-1.2 \\ =2.5e^{\mleft\{-0.18\mright\}}-0.9-1.2 \\ =2.5\cdot(1)/(e^(0.18))-2.1 \\ =-0.01 \end{gathered}`

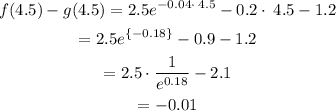
The second value on the right side of the table is the one we just got.

Upper bound:

`\begin{gathered} f(5)-g(5)=2.5e^(-0.04\cdot\: 5)-0.2\cdot\: 5-1.2 \\ =2.5e^{\mleft\{-0.2\mright\}}-1-1.2 \\ =2.5\cdot(1)/(e^(0.2))-2.2 \\ =-0.15 \end{gathered}`

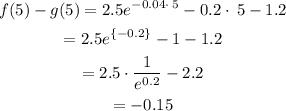
The third value on the right side of the table is the one we just got.