Question

Find p if the coefficient of x^2 in the expansion of (1+2x)(2+px)^5 is 1200.

A. 7
B. 8
C. 9
D. 10.

Answer 1

The value of p that satisfies the condition is 10. The answer is D. 10.

Step-by-step explanation:

To find the coefficient of x^2 in the expansion of (1+2x)(2+px)^5, we can use the binomial theorem. The binomial theorem states that for any positive integer n, the expansion of (a + b)^n can be written as:

`(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + C(n, 2) * a^(n-2) * b^2 + ... + C(n, n-2) * a^2 * b^(n-2) + C(n, n-1) * a^1 * b^(n-1) + C(n, n) * a^0 * b^n`

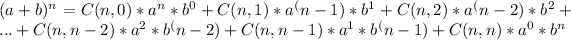
Where C(n, k) represents the binomial coefficient, which is the number of ways to choose k items from a set of n items.

In our case, we have (1+2x) as a, and (2+px) as b. We need to find the coefficient of x^2, so we are interested in the term with b^2.

Expanding (1+2x)(2+px)^5 using the binomial theorem, we get:

`(1+2x)(2+px)^5 = C(5, 0) * (1^5) * (2^0) * (2+px)^5 + C(5, 1) * (1^4) * (2^1) * (2+px)^4 * (px) + C(5, 2) * (1^3) * (2^2) * (2+px)^3 * (px)^2 + ... + C(5, 4) * (1^1) * (2^4) * (2+px) * (px)^4 + C(5, 5) * (1^0) * (2^5) * (px)^5`

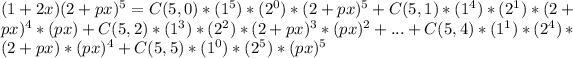
We are interested in the term with (px)^2. Looking at the expansion, we see that this term is obtained from the C(5, 2) * (1^3) * (2^2) * (2+px)^3 * (px)^2 term.

The coefficient of x^2 is obtained by multiplying the coefficients of (2+px)^3 and (px)^2. In other words, we need to find the coefficient of x in the expansion of (2+px)^3 and then multiply it by C(5, 2).

Using the binomial theorem for (2+px)^3, we get:

`(2+px)^3 = C(3, 0) * (2^3) * (px)^0 + C(3, 1) * (2^2) * (px)^1 + C(3, 2) * (2^1) * (px)^2 + C(3, 3) * (2^0) * (px)^3`

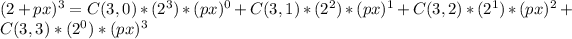
The coefficient of x in this expansion is obtained from the C(3, 1) * (2^2) * (px)^1 term, which is 3 * 4 * p = 12p.

Now, we multiply this coefficient by C(5, 2) to get the coefficient of x^2:

Coefficient of x^2 = C(5, 2) * 12p = 10 * 12p = 120p

We know that the coefficient of x^2 is 1200, so we can set up the equation:

120p = 1200

Dividing both sides by 120, we get:

p = 10

Therefore, the value of p that satisfies the condition is 10.

The answer is D. 10.