Let's draw the points in the 2-D space:
To prove it is a parallelogram, we need to prove that lines AD and BC are parallel to each other, and lines AB and DC are also parallel to each other.
We can prove that by calculating the slopes of the lines.
The slope of the line passing through points (x₁,y₁) and (x₂,y₂) is calculated through the following formula:

Let's begin with segment AB.
A = (0,0), B = (2,-1)
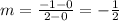
For segment DC:
D = (4,5), C = (6,4)
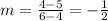
Segments AB and DC have the same slope, therefore they are parallel.
Now let's prove for points AD and BC.
For segmen AD, A = (0,0), D = (4,5)
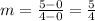
For segment BC:
B = (2,-1), C = (6,4)

The slope of segments AD and BC is the same, therefore, segments AD and BC are parallel.
Now we have proved that the opposite sides of the figure formed by joining the 4 points are parallel to each other, by comparing their slopes. The figure is indeed a parallelogram.