Question

I need help figuring out the work by the force on block, the work done by gravity on the block and the magnitude of the normal force between the block and the wall

Answer 1

We are given that a block is pushed upwards vertically by a force that has an angle of 25 degrees. To determine the work done by the force "F" we will first add the forces in the vertical direction:

`\Sigma F_v=F_v-mg-F_f`

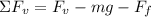
Where:

`\begin{gathered} F_v=\text{ vertical component of the force} \\ m=\text{ mass of the block} \\ F_f=\text{ friction force} \\ g=\text{ acceleration of gravity} \end{gathered}`

Now, we determine the vertical component of the force. To do that we will use the trigonometric function sine since it is defined as:

`\sin 25=(F_v)/(F)`

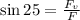
Now we multiply both sides by the force "F":

`F\sin 25=F_v`

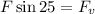
Now we replace this in the sum of vertical forces:

`\Sigma F_v=F\sin 25-mg-F_f`

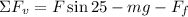
To determine the friction force we will use the following relationship:

`F_f=\mu N`

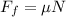
Where:

`\begin{gathered} \mu=\text{ coefficient of friction} \\ N=\text{ normal force} \end{gathered}`

The coefficient of friction is given therefore, we need to determine the magnitude of the normal force. To do that we will add the forces in the horizontal direction:

`\Sigma F_h=N-F_h`

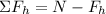
We determine the horizontal component of the force using the trigonometric function cosine:

`\cos 25=(F_h)/(F)`

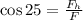
Now we multiply both sides by "F":

`F\cos 25=F_h`

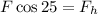
Now we substitute in the sum of forces:

`\Sigma F_h=N-F\cos 25`

Since there is no movement in the horizontal direction the sum of the forces must be equal to zero:

`N-F\cos 25=0`

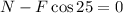
Now we solve for N by adding "Fcos25" to both sides:

`N=F\cos 25`

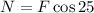
Now we substitute this value in the relationship for friction:

`F_f=\mu F\cos 25`

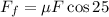
Now we substitute the friction force in the vertical sum of forces:

`\Sigma F_v=F\sin 25-mg-\mu F\cos 25`

Since the velocity is constant this means that the acceleration is zero and therefore, the sum of the forces is zero:

`F\sin 25-mg-\mu F\cos 25=0`

Now we solve for "F". To do that we will add "mg" to both sides:

`F\sin 25-\mu F\cos 25=mg`

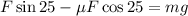
Now we take "F" as a common factor:

`F(\sin 25-\mu\cos 25)=mg`

Now we divide by the factor of "F":

`F=(mg)/(\sin25-\mu\cos25)`

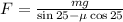
Now we substitute the given values:

`F=((5kg)(9.8(m)/(s^2)))/(\sin 25-(0.3)\cos 25)`

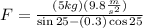
Solving the operations:

`F=325.42N`

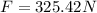
Now, to determine the work done by the force we use the following formula:

`W=Fd`

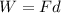
Where:

`\begin{gathered} F=\text{ force} \\ d=\text{ distance} \end{gathered}`

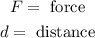
Substituting the values we get:

`W=(325.42N)(3m)=976.27J`

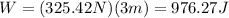
Therefore, the work done by the force is 976.27 Joules.

Now we determine the work done by gravity. This is equivalent to the work done by the weight therefore, it is:

`W_g=\text{mgd}`

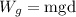
Where "m" is mass, and "g" is the acceleration of gravity. Their product is the weight.

Substituting the values:

Solving we get:

`W_g=147.15J`

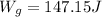
The magnitude of the work done by gravity is 147.15 Joules.

Finally, to determine the normal force we use the equation we got from the sum of forces in the horizontal direction:

`N=F\cos 25`

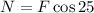
Now we substitute the value we found for "F":

`N=(325.42N)(\cos 25)=294.93N`

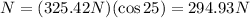
Therefore, the normal force is 294.93 Newtons.