The length of the arc subtended by an angle θ with a radius r can be computed using the equation
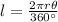
a) On the first problem, the radius of the circle is 4 cm while the degree angle of the arc subtended is 50°. Just substitute these values on the equation above and solve. We get
![\begin{gathered} l=(2\pi(4cm)(50^(\circ)))/(360^(\circ)) \\ l=(10)/(9)\pi\approx3.5\operatorname{cm} \end{gathered}]()
b) We can see that from the equation to solve the arc length, the length is proportional with the radius of the circle, hence, the longer the radius of the circle, the longer the arc length.
c) Using the same working idea to solve the arc length of the circle on the problem (a), we have
![\begin{gathered} l=(2\pi(6cm)(50^(\circ)))/(360^(\circ)) \\ l=(5)/(3)\pi\approx5.2\operatorname{cm} \end{gathered}]()
As you can see, a longer arc length is observed in a 6 cm circle than on a 4 cm circle.