Question

Write the first five terms of the geometric sequence in which a1=34 and the common ration is r= -1/2

Answer 1

The formula used to calculate the nth term of a geometric sequence is given to be:

`a_n=a_1\cdot r^(n-1)`

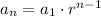
From the question, we are given the following parameters:

`\begin{gathered} a_1=34 \\ r=-(1)/(2) \end{gathered}`

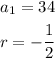
Therefore, we can calculate the first 5 terms as follows:

First Term: 34

Second Term: -17

`\begin{gathered} n=2 \\ \therefore \\ a_2=34(-(1)/(2))^(2-1)=34*(-(1)/(2)) \\ a_2=-17 \end{gathered}`

Third Term: 8.5

`\begin{gathered} n=3 \\ \therefore \\ a_3=34(-(1)/(2))^(3-1)=34*(1)/(4) \\ a_3=8.5 \end{gathered}`

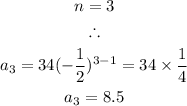
Fourth Term: -4.25

`\begin{gathered} n=4 \\ \therefore \\ a_4=34(-(1)/(2))^(4-1)=34*(-(1)/(2))^3=34*(-(1)/(8)) \\ a_4=-4.25 \end{gathered}`

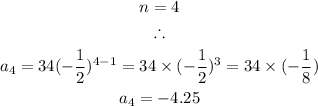
Fifth Term:

`\begin{gathered} n=5 \\ \therefore \\ a_5=34(-(1)/(2))^(5-1)=34*(-(1)/(2))^4=34*(1)/(16) \\ a_5=2.125 \end{gathered}`

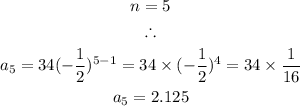
The first five terms are 34, -17, 8.5, -4.25, and 2.125.