Question

Solve the system of equations
x2 + 2y2 + 4y - 70=0
X2 + 1472 - 687 - 10=0

Answer 1

The solution to the system of equations is (x₁, y₁) = (0, 1) and (x₂, y₂) = (0, 5).

How to solve a system of nonlinear equations

In this problem we find the case of a system of equations formed by conics, which can be solved both by analytic approach and by graphic approach. We proceed to use the analytic approach:

Step 1 - Eliminate x² on both expressions:

2 · y² + 4 · y - 70 = 14 · y² - 68 · y - 10

Step 2 - Simplify the expression until a quadratic equation is found:

12 · y² - 72 · y + 60 = 0

y² - 6 · y + 5 = 0

Step 3 - Factor the quadratic equation:

(y - 5) · (y - 1) = 0

y = 5 or y = 1

Step 4 - Find all values of x:

x² = 2 · y² + 4 · y - 70

`x = √(2\cdot y^2 + 4\cdot y - 70)`

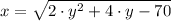
y = 5:

`x = √(2\cdot 5^2 + 4\cdot 5 - 70)`

x = 0

y = 1

`x = √(2\cdot 1^2 + 4\cdot 1 - 70)`

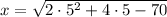
x = 0

Step 5 - Write all the solution to the system of equations:

(x₁, y₁) = (0, 1) and (x₂, y₂) = (0, 5)

Remark

The statement presents typing mistakes, correct form is introduced below:

Solve the system of equations:

x² + 2 · y² + 4 · y - 70 = 0

x² + 14 · y² - 68 · y - 10 = 0