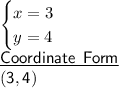Question

I need help 6x-2y=10 x-2y=-5 solve by elimination

Answer 1

Step-by-step explanation

• Given the system of equations.

`\begin{cases} 6x - 2y = 10 \\ x - 2y = - 5 \end{cases}`

• Solve the system of equations by eliminating either x-term or y-term. We will eliminate the y-term as it is faster to solve the equation.

To eliminate the y-term, we have to multiply the negative in either the first or second equation so we can get rid of the y-term. I will multiply negative in the second equation.

`\begin{cases} 6x - 2y = 10 \\ - x + 2y = 5 \end{cases}`

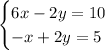
There as we can get rid of the y-term by adding both equations.

`(6x - x) + ( - 2y + 2y) = 10 + 5 \\ 5x + 0 = 15 \\ 5x = 15 \\ x = (15)/(5) \longrightarrow \frac{ \cancel{15}}{ \cancel{5}} = (3)/(1) \\ x = 3`

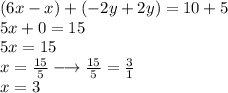
Hence, the value of x is 3. But we are not finished yet because we need to find the value of y as well. Therefore, we substitute the value of x in any given equations. I will substitute the value of x in the second equation.

`x - 2y = - 5 \\ 3 - 2y = - 5 \\ 3 + 5 = 2y \\ 8 = 2y \\ (8)/(2) = y \\ y = (8)/(2) \longrightarrow \frac{ \cancel{8}}{ \cancel{2}} = (4)/(1) \\ y = 4`

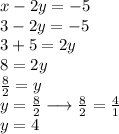
Hence, the value of y is 4. Therefore, we can say that when x = 3, y = 4.

• Answer Check by substituting both x and y values in both equations.

First Equation

`6x - 2y = 10 \\ 6(3) - 2(4) = 10 \\ 18 - 8 = 10 \\ 10 = 10 \longrightarrow \sf{true} \: \green{ \checkmark}`

Second Equation

`x - 2y = - 5 \\ 3 - 2(4) = - 5 \\ 3 - 8 = - 5 \\ - 5 = - 5 \longrightarrow \sf{true} \: \green{ \checkmark}`

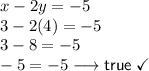
Hence, both equations are true for x = 3 and y = 4. Therefore, the solution is (3,4)

Answer

`\begin{cases} x = 3 \\ y = 4 \end{cases} \\ \sf \underline{Coordinate \: \: Form} \\ (3,4)`