Question

What is the vertex of y=-x^2+12x-31?????

Answer 1

Step-by-step explanation

• Formulas for finding the vertex.

`h = - (b)/(2a) \\ k = \frac{4ac - {b}^(2) }{4a}`

• Vertex Form

`y = a{(x - h)}^(2) + k`

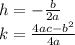
Where the a-term determines how wide, narrow, upward or downward the graph is.

The h-term determines the horizontal shift of graph. (x-axis)

The k-term determines the vertical shift of graph. (y-axis)

The vertex of graph is at (h,k). We can find the vertex by using the given formulas.

• Find the vertex

From the equation, the coefficients are:

`\begin{cases} a = - 1 \\ b = 12 \\ c = - 31 \end{cases}`

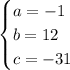
Substitute these values in the formulas.

Find the value of h

`h = - (12)/(2( - 1)) \\ h = - (12)/( - 2) \\ h = - ( - 6)/(1) \longrightarrow - ( - 6) = 6 \\ h = 6`

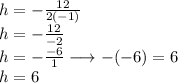
Hence, the value of h is 6.

Find the value of k

`k = \frac{4( - 1)( - 31) - {(12)}^(2) }{4( - 1)} \\ k = (124 - 144)/( - 4) \\ k = ( - 20)/( - 4) \longrightarrow (5)/(1) = 5 \\ k = 5`

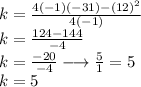
Hence, the value of k is 5. Then we substitute both value of h and k in the vertex form

• Rewrite the equation of vertex form by substituting the value of h and k

`y = a {(x - h)}^(2) + k \\ y = - 1 {(x - 6)}^(2) + 5 \\ y = - {(x - 6)}^(2) + 5`

Answer

Since the vertex is at (h,k). Therefore the value of h is 6 and k is 5. Therefore:

`\large{(h, k)=(6, 5)}`

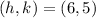
(6,5) is the vertex.