Answer:
(A) f(x) = 2 *

Explanation:
[] We can find our answer by plugging the x values into the functions as t and solving.
-. Using this method, starting with the A function, we find that the first function models the data and we do not need to test the others. I still have shown the work for the others as it is good to check your work.
[✓] f(x) = 2 *

(1, 8) }{}{}{ f(x) = 2 *
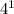 = 2 * 4 = 8
= 2 * 4 = 8
(2, 32) }{}{}{ f(x) = 2 *
 = 2 * 16 = 32
= 2 * 16 = 32
(3, 128) }{}{}{ f(x) = 2 *
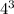 = 2 * 64 = 128
= 2 * 64 = 128
-> This pattern continues
[✗] f(x) =

(1, 8) }{}{}{ f(x) =
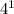 = 4 ≠ 8
= 4 ≠ 8
-> This function does not model the data as it does not fulfil the first point
[✗] f(x) = 4 *
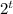
(1, 8) }{}{}{ f(x) = 4 *
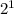 = 4 * 2 = 8
= 4 * 2 = 8
(2, 32) }{}{}{ f(x) = 4 *
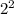 = 4 * 4 = 16 ≠ 32
= 4 * 4 = 16 ≠ 32
-> This function only models (1, 8) but does not fully model the data
[✗] f(x) =
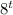
(1, 8) }{}{}{ f(x) =
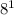 = 8
= 8
(2, 32) }{}{}{ f(x) =
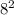 = 64 ≠ 32
= 64 ≠ 32
-> This function only models (1, 8) but does not fully model the data
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather