Question

Which of the following ordered pairs is not a solution of the system of inequalities?y > x2 – 4x – 5y < –x2 – 5x + 6Question 6 options:A) (1, –5)B) (–1, 6)C) (1, 7)D) (1, –7)

Answer 1

In this problem, we have the following system of inequalities:

`\begin{gathered} y>x^2-4x-5, \\ y<-x^2-5x+6. \end{gathered}`

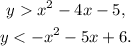
We must check which of the given pair of values (x, y) is not a solution of the system. To do that, we replace the values (x, y) in the system, and then we check if the inequality holds.

A) Replacing (x, y) = (1, -5), we have:

`\begin{gathered} -5>1^2-4\cdot1-5=-8\Rightarrow-5>-8\text{ }✓ \\ -5<-1^2-5\cdot1+6=0\Rightarrow-5<0\text{ }✓ \end{gathered}`

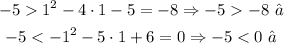
B) Replacing (x, y) = (-1, 6), we have:

`\begin{gathered} 6>(-1)^2-4\cdot(-1)-5=0\Rightarrow6>0\text{ }✓ \\ 6<-(-1)^2-5\cdot(-1)+6=10\Rightarrow6<10\text{ }✓ \end{gathered}`

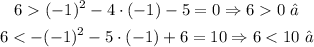
C) Replacing (x, y) = (1, 7), we have:

`\begin{gathered} 7>1^2-4\cdot1-5=-8\Rightarrow7>-8\text{ }✓ \\ 7<-1^2-5\cdot1+6=0\Rightarrow7<0\text{ }✖ \end{gathered}`

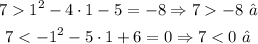
We see that the second inequality doesn't hold. So the ordered pair (1, 7) is not a solution of the system.

D) Replacing (x, y) = (1, -7), we have:

`\begin{gathered} -7>1^2-4\cdot1-5=-8\text{ }✓ \\ -7<-1^2-5\cdot1+6=0\text{ }✓ \end{gathered}`

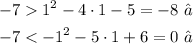
Answer

C) (1, 7)