Question

Use the given graph to create the equation for the rational function. The function is written in factored form and help see how they given information shapes or equations

Answer 1

Given the graph of the rational function:

As shown there are two asymptotes

The lines of the asymptotes are:

x = -3, x = 2

So. the factors of the denominator are:

`(x+3),(x-2)`

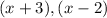
Note: (x - 2) will be repeated

And the function has an x-intercept at the point x = 1

So, the factor of the numerator will be (x - 1)

So, the function will have the following form:

`f(x)=(a(x-1)^2)/((x+3)(x-2)(x-2))`

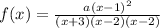
we will find the value of (a) using the point of the y-intercept

As shown the y-intercept = (0, -1/2)

So, substitute with x = 0, f = -1/2

`\begin{gathered} -(1)/(2)=(a\cdot(-1)^2)/(3\cdot(-2)\cdot(-2)) \\ a=-(1)/(2)\cdot3\cdot(-2)\cdot(-2)=-6 \end{gathered}`

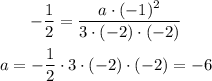
So, the answer will be:

The numerator is: -6 (x - 1)²

The denominator is: ( x + 3) ( x - 2 ) (x - 2)