Question

Solve the following word problems by creating and solving systems of equations.1) A plane traveled 1290 miles with the wind (downwind) for 3 hours. Then it traveled 1576 miles against thewind (upwind) for 4 hours. Find the speed of the plane in still air and the speed of the wind.

Answer 1

The speed of the plane = 412 miles per hour

The speed of the wind = 18 miles per hour.

Step-by-step explanation:

Let's call x the speed of the plane and y the speed of the wind.

Then, the distance that a plane traveled can be calculated as:

`d=v\cdot t`

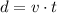
Where v is the sum of the speed of the plane and the speed of the wind and t is the number of hours.

Now, if the plane traveled 1290 miles with the wind (downwind) for 3 hours, we can write the following equation:

`1290=(x+y)\cdot3^{}`

In the same way, if the plane traveled 1576 miles against the wind (upwind) for 4 hours, we get:

`1576=(x-y)\cdot4`

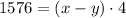
So, the systems of equations is equal to:

1290 = 3(x + y)

1576 = 4(x - y)

Solving for x in the first equation, we get:

`\begin{gathered} (1290)/(3)=(3(x+y))/(3) \\ 430=x+y \\ 430-y=x+y-y \\ 430-y=x \end{gathered}`

Now, we can substitute x = 430 - y on the second equation and solve for y:

`\begin{gathered} 1576=4((430-y)-y_{}) \\ 1576=4(430-2y) \\ (1576)/(4)=(4(430-2y))/(4) \\ 394=430-2y \\ 394-430=430-2y-430 \\ -36=-2y \\ (-36)/(-2)=(-2y)/(-2) \\ 18=y \end{gathered}`

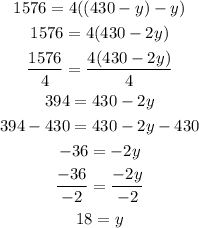
Finally, we can calculate the value of x:

`\begin{gathered} x=430-y \\ x=430-18 \\ x=412 \end{gathered}`

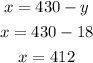
Therefore, the speed of the plane is 412 miles per hour and the speed of the wind is 18 miles per hour.