Answer:
See Below.
Explanation:
Statements: Reasons:
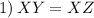 Given
Given
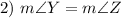 Isosceles Triangle Theorem
Isosceles Triangle Theorem
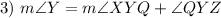 Angle Addition
Angle Addition
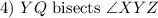 Given
Given
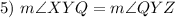 Definition of Bisector
Definition of Bisector
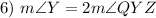 Substitution
Substitution
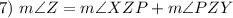 Angle Addition
Angle Addition
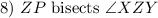 Given
Given
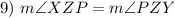 Definition of Bisector
Definition of Bisector
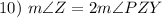 Substitution
Substitution
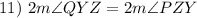 Substitution
Substitution
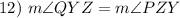 Division Property of Equality
Division Property of Equality
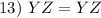 Reflexive Property
Reflexive Property
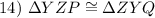 Angle-Side-Angle Congruence*
Angle-Side-Angle Congruence*
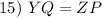 CPCTC
CPCTC
*For clarification:
∠Y = ∠Z
YZ = YZ (or ZY)
∠PZY = ∠QYZ
So, Angle-Side-Angle Congruence:
ΔYZP is congruent to ΔZYQ