Question

2. Adult female Dalmatians have a mean weight of 50 lbs and a standard deviation of 3.3 lbs.Assume the weights are normally distributed.a) Find the z-score of an adult female Dalmatian who weighs 60 lbs.b) Find the Z-score of an adult female Dalmatian whose weight is 30 lbs below the mean.c) Find the weight of an adult female Dalmatian whose weight is 1.75 standard deviationsabove the mean weight.

Answer 1

The answers are :

a. 3.03

b. -9.09

c. 55.775 lbs

EXPLANATION :

The z-score formula is :

`\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{ where :} \\ \text{ x = sample weight} \\ \mu\text{ = mean weight} \\ \sigma\text{ = standard deviation} \end{gathered}`

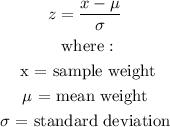
From the problem, we have :

`\mu=50\text{ }lbs\quad and\quad\sigma=3.3\text{ }lbs`

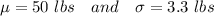
a. z-score when x = 60 lbs.

That will be :

`\begin{gathered} z=(60-50)/(3.3) \\ z=3.03 \end{gathered}`

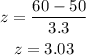
b. z-score when x = 30 lbs below the mean, the mean weight is 50 lbs, so it will be x = 50 - 30 = 20

The z-score will be :

`\begin{gathered} z=(20-50)/(3.3) \\ z=-9.09 \end{gathered}`

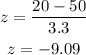
c. weight when it is 1.75 standard deviations above the mean weight.

Above the mean weight denotes that the z-score is positive.

Substitute z = 1.75 and solve for x :

`\begin{gathered} 1.75=(x-50)/(3.3) \\ 1.75(3.3)=x-50 \\ x=1.75(3.3)+50 \\ x=55.775 \end{gathered}`