We are given that two protons are 7.1818 fm apart. To determine the electric force between them we need to use the following formula:
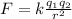
Where:
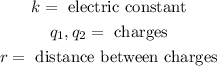
The charge of a proton is:
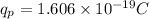
Now, we plug in the values:
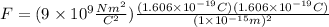
Solving the operations:

Now, we need to determine the gravitational force. We will use the following formula:
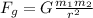
Where;
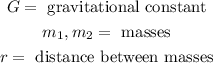
The mass of a proton is given by:
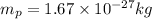
Now, we plug in the values:
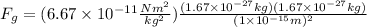
Solving the operations:
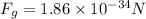
Now, we determine the ratio between the forces:
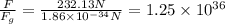
This means that the electric force is 1.25 by ten to the 36th times larger than the gravitational force.