Question

In the aerobic degradation of C3H6O3, represented by the equation C3H6O3 + a O2 + b NH3 Æ c C5H7NO2 + d H2O + e CO2, determine the values for a, b, c, d, and e if YX/S = 0.4 g X/g S.

a. a = 4, b = 9, c = 3, d = 4, e = 5
b. a = 6, b = 4, c = 5, d = 3, e = 2
c. a = 3, b = 5, c = 7, d = 2, e = 6
d. a = 2, b = 7, c = 6, d = 5, e = 3

Answer 1

The given problem involves determining the values for
`\(a, b, c, d,\) and \(e\)` in the chemical equation
`\(C_3H_6O_3 + a \, O_2 + b \, NH_3 \rightarrow c \, C_5H_7NO_2 + d \, H_2O + e \, CO_2\)` based on the provided yield coefficient
`\(Y_(X/S) = 0.4 \, g X/g S\).`

Options A, B, C and D are none of the correct ones

Step-by-step explanation:

To determine the values for
`\(a, b, c, d, \) and \(e\)`, we can use the stoichiometry of the given chemical equation and the yield coefficient
`\(Y_(X/S).\)`

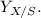
The given equation is:

`\[ C_3H_6O_3 + a \, O_2 + b \, NH_3 \rightarrow c \, C_5H_7NO_2 + d \, H_2O + e \, CO_2 \]`

The yield coefficient
`\(Y_(X/S)\)` is defined as the amount of biomass
`(\(X\))` produced per unit of substrate
`(\(S\))` consumed. In this case,
`\(Y_(X/S) = 0.4 \, g X/g S.\)`

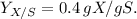
The molecular weight of \(C_3H_6O_3\) is approximately 90 g/mol.

Now, let's balance the equation using the given options:

a.
`\(a = 4, b = 9, c = 3, d = 4, e = 5\)`

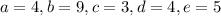
`\[\text{C}_3\text{H}_6\text{O}_3 + 4 \, \text{O}_2 + 9 \, \text{NH}_3 \rightarrow 3 \, \text{C}_5\text{H}_7\text{NO}_2 + 4 \, \text{H}_2\text{O} + 5 \, \text{CO}_2\]`

Now, let's check if the yield coefficient
`\(Y_(X/S)\)` is satisfied:

`\[ Y_(X/S) = \frac{\text{moles of } C_5H_7NO_2}{\text{moles of } C_3H_6O_3} = \frac{3 * \text{MW}_(C_5H_7NO_2)}{\text{MW}_(C_3H_6O_3)} = (3 * 113)/(90) \]`

However, this does not equal 0.4, so option a is not correct.

b.
`\(a = 6, b = 4, c = 5, d = 3, e = 2\)`

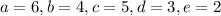
`\[\text{C}_3\text{H}_6\text{O}_3 + 6 \, \text{O}_2 + 4 \, \text{NH}_3 \rightarrow 5 \, \text{C}_5\text{H}_7\text{NO}_2 + 3 \, \text{H}_2\text{O} + 2 \, \text{CO}_2\]`

Now, let's check if the yield coefficient
`\(Y_(X/S)\)` is satisfied:

`\[ Y_(X/S) = \frac{\text{moles of } C_5H_7NO_2}{\text{moles of } C_3H_6O_3} = \frac{5 * \text{MW}_(C_5H_7NO_2)}{\text{MW}_(C_3H_6O_3)} = (5 * 113)/(90) \]`

This value does not equal 0.4 either, so option b is not correct.

c.
`\(a = 3, b = 5, c = 7, d = 2, e = 6\)`

`\[\text{C}_3\text{H}_6\text{O}_3 + 3 \, \text{O}_2 + 5 \, \text{NH}_3 \rightarrow 7 \, \text{C}_5\text{H}_7\text{NO}_2 + 2 \, \text{H}_2\text{O} + 6 \, \text{CO}_2\]`

Now, let's check if the yield coefficient
`\(Y_(X/S)\)` is satisfied:

`\[ Y_(X/S) = \frac{\text{moles of } C_5H_7NO_2}{\text{moles of } C_3H_6O_3} = \frac{7 * \text{MW}_(C_5H_7NO_2)}{\text{MW}_(C_3H_6O_3)} = (7 * 113)/(90) \]`

This value does not equal 0.4 either, so option c is not correct.

d.
`\(a = 2, b = 7, c = 6, d = 5, e = 3\)`

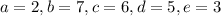
`\[\text{C}_3\text{H}_6\text{O}_3 + 2 \, \text{O}_2 + 7 \, \text{NH}_3 \rightarrow 6 \, \text{C}_5\text{H}_7\text{NO}_2 + 5 \, \text{H}_2\text{O} + 3 \, \text{CO}_2\]`

Now, let's check if the yield coefficient
`\(Y_(X/S)\)` is satisfied:

`\[ Y_(X/S) = \frac{\text{moles of } C_5H_7NO_2}{\text{moles of } C_3H_6O_3} = \frac{6 * \text{MW}_(C_5H_7NO_2)}{\text{MW}_(C_3H_6O_3)} = (6 * 113)/(90) \]`

This value does not equal 0.4 either, so option d is not correct.

Options A, B, C and D are none of the correct ones