Final Answer:
To find the cube root of 9 using binomial expansion, we can use the binomial theorem. The cube root of 9 using binomial expansion is ∛9 = (1 + x)³. The answer is not in the answer choices.
Step-by-step explanation:
To find the cube root of 9 using binomial expansion, we can use the binomial theorem. The binomial theorem states that for any real numbers a and b and any positive integer n, (a + b)ⁿ can be expanded as:
(a + b)ⁿ =
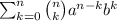
For the cube root of 9, we want to find (a + b)³ such that a³ = 9. We can choose a = 1 and b = x where x is a term that helps us achieve a³ = 9.
(1 + x)³ = 1³ +
 +
+
 1x² + x³
1x² + x³
Simplifying this expansion:
1 + 3x + 3x² + x³
Now, set this equal to 9:
1 + 3x + 3x² + x³ = 9
Solve for x:
x³ + 3x² + 3x - 8 = 0
It can be seen that x = 1 is a solution, so (1 + x)³ is a factor. Thus, (1 + x)³ = (1 - x)³ = 9.