Question

Express each of the following trigonometric functions in terms of surds.a) cos (7/4 π)b) tan 240°

Answer 1

Step-by-step explanation:

a) cos (7/4π)

We simplify the given trigonometric function first to express it into a surd. Surd means when we can't simplify a number to remove a square root or has a decimal which goes on forever without repeating.

For the given the given function:

`\begin{gathered} \cos ((7)/(4)\pi)=\cos (\pi+(3\pi)/(4)) \\ \\ \\ \end{gathered}`

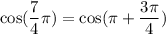
Using the identity:

cos(x+y)=cos(x)cos(y)-sin(x)sin(y)

So,

`\begin{gathered} =\cos (\pi)\cos ((3\pi)/(4))-\sin (\pi)\sin ((3\pi)/(4)) \\ \end{gathered}`

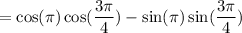
Since:

`\begin{gathered} \cos (\pi)=-1 \\ \sin (\pi)=0 \\ \cos ((3\pi)/(4))=-\frac{\sqrt[]{2}}{2} \\ \sin ((3\pi)/(4))=\frac{\sqrt[]{2}}{2} \end{gathered}`

Simplify and rearrange

`\begin{gathered} =\cos (\pi)\cos ((3\pi)/(4))-\sin (\pi)\sin ((3\pi)/(4)) \\ =(-1)(-\frac{\sqrt[]{2}}{2})-(0)(\frac{\sqrt[]{2}}{2}) \\ \text{Calculate} \\ =\frac{\sqrt[]{2}}{2} \end{gathered}`

Therefore,

`\cos ((7\pi)/(4))=\frac{\sqrt[]{2}}{2}`