Answer:
Step-by-step explanation:
a) cos (7/4π)
We simplify the given trigonometric function first to express it into a surd. Surd means when we can't simplify a number to remove a square root or has a decimal which goes on forever without repeating.
For the given the given function:

Using the identity:
cos(x+y)=cos(x)cos(y)-sin(x)sin(y)
So,
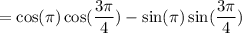
Since:
![\begin{gathered} \cos (\pi)=-1 \\ \sin (\pi)=0 \\ \cos ((3\pi)/(4))=-\frac{\sqrt[]{2}}{2} \\ \sin ((3\pi)/(4))=\frac{\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/b80vm9obfamkcjclwbap.png)
Simplify and rearrange
![\begin{gathered} =\cos (\pi)\cos ((3\pi)/(4))-\sin (\pi)\sin ((3\pi)/(4)) \\ =(-1)(-\frac{\sqrt[]{2}}{2})-(0)(\frac{\sqrt[]{2}}{2}) \\ \text{Calculate} \\ =\frac{\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ri4ryerv4rjk3sp9mx5t.png)
Therefore,
![\cos ((7\pi)/(4))=\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/s309uk46f164ied7f3qn.png)