Question

Look at photo for accurate description round to the nearest integer as needed

Answer 1

Given two angles and one side of the triangle, you have to find the missing angle and the missing sides.

To do it, you can follow the steps.

Step 1: Find the missing angle.

Knowing that the sum of interior angles of a triangle is 180°, you can find A.

A + B + C = 180°

Knowing that B = 42° and C = 100°, you can substitute them in the equation and find A.

A + 42 + 100 = 180

A + 142 = 180

Adding - 142 to both sides:

A + 142 - 142 = 180 - 142

A + 0 = 38

A = 38°

Step 2: Find the missing sides.

Since all the angles and only one side are known, you can use the sen rule.

`(a)/(\sin(A))=(b)/(\sin(B))=(c)/(\sin(C))`

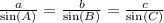
Substituting the values, you have:

`(a)/(\sin(38))=(165)/(\sin(42))=(c)/(\sin(100))`

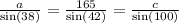
First, let's compare sides a and b:

`(a)/(\sin(38))=(165)/(\sin(42))`

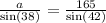
Multiplying both sides bi sin(38):

`\begin{gathered} (a)/(\sin(38))\cdot\sin (38)=(165)/(\sin(42))\cdot\sin (38) \\ a=165\cdot(\sin(38))/(\sin(42)) \end{gathered}`

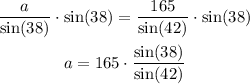
And solving the equation:

`\begin{gathered} a=165\cdot(0.6157)/(0.6691) \\ a=151.8 \end{gathered}`

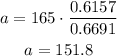
Now, let's find c by comparing b and c:

`(c)/(\sin(100))=(165)/(\sin(42))`

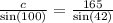
Multiplying both sides by sin(100) and solving the equation.

`\begin{gathered} (c)/(\sin(100))\cdot\sin (100)=(165)/(\sin(42))\cdot\sin (100) \\ c=165\cdot(\sin (100))/(\sin (42)) \\ c=165\cdot(0.9848)/(0.6691) \\ c=242.8 \end{gathered}`

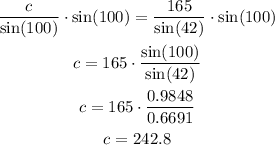
Done! You found the missing sides and angles.

As you can see, there is only one possible solution.

And the solution is:

a = 151.8; A = 38°

b = 165; B = 42°

c = 242.8; C = 100°