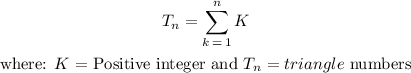Triangular numbers are a pattern of numbers that form equilateral triangles. Each subsequent number in the sequence adds a new row of dots to the triangle.
In each case, the number of dots in the lower row increases by 1. We can depict this by:
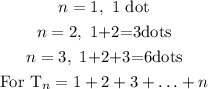
Therefore, putting this in summation form gives: