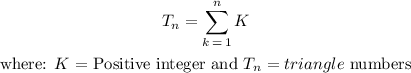Question

Find a formula for T(n), the nth triangular number (starting with n = 1).

Answer 1

Triangular numbers are a pattern of numbers that form equilateral triangles. Each subsequent number in the sequence adds a new row of dots to the triangle.

In each case, the number of dots in the lower row increases by 1. We can depict this by:

`\begin{gathered} n=1,\text{ }1\text{ dot} \\ n=2,\text{ 1+2=3dots} \\ n=3,\text{ 1+2+3=6dots} \\ \text{For T}_n=1+2+3+\ldots+n \end{gathered}`

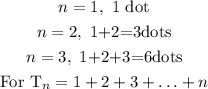
Therefore, putting this in summation form gives:

`\begin{gathered} T_n=\sum ^n_(k\mathop=1)K \\ \text{where: }K\text{ = Positive integer and }T_n=triangle\text{ numbers} \end{gathered}`