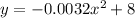Question

Find the equation for a parabola that is 100ft wide and 8 ft tall and so downwards openings

Answer 1

Step-by-step explanation

We are given that:

An arch that supports a bridge is built in the shape of a downwards opening parabola. Its span is 100 ft and max height is 8 ft.

We are required to find the equation of the parabola that models the situation.

First, we use the form of the general equation of a parabola:

`y=ax^2+bx+c`

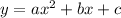
Let the axis of symmetry be x = 0, and the y-intercept is the maximum height = 8 ft. Thus:

`\begin{gathered} x\text{ }intercepts\to(-50,0)\text{ }and\text{ }(50,0) \\ y\text{ }intercept\text{ }(c)=8 \end{gathered}`

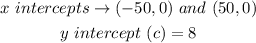
Next, we substitute the x-intercepts in the general form as follows:

`\begin{gathered} y=ax^(2)+bx+c \\ when\text{ }(x,y)\to(-50,0) \\ 0=a(-50)^2+b(-50)+8 \\ 2500a-50b=-8\text{ }(equation\text{ }1) \\ \\ when\text{ }(x,y)\to(50,0) \\ 0=a(50)^2+b(50)+8 \\ 2500a+50b=-8\text{ }(equation\text{ }2) \\ \\ Equation\text{ }1+Equation\text{ }2 \\ 5000a=-16 \\ a=-(16)/(5000)=-0.0032 \\ \\ From\text{ }equation\text{ }2 \\ \begin{equation*} 2500a+50b=-8 \end{equation*} \\ Substitute\text{ }for\text{ }a \\ 2500(-0.0032)+50b=-8 \\ -8+50b=-8 \\ 50b=0 \\ b=(0)/(50) \\ b=0 \end{gathered}`

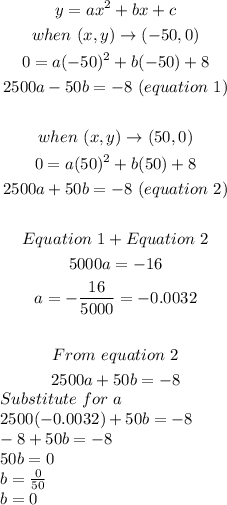
Finally, substituting the values of a, b, and c in the general form, we have:

`\begin{gathered} y=ax^2+bx+c \\ y=-0.0032x^2+0x+8 \\ y=-0.0032x^2+8 \end{gathered}`

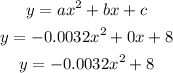
Graphing this function, we have:

Hence, the answer is:

`y=-0.0032x^2+8`