Question

Calculate the speed (in km/sec) of an asteroid in a circular orbit at 4 AU by dividing the orbit’s circumference by its period.

Answer 1

Given:

The radius of the orbit of the asteroid, R=4 AU

To find:

The orbital speed of the asteroid.

Step-by-step explanation:

1 AU=1.5×10¹¹ m

Thus the radius of the orbit in meters is given by,

`\begin{gathered} R=4*1.5*10^(11) \\ =6*10^(11)\text{ m} \end{gathered}`

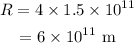
The orbital period is given by,

`T=2\pi\sqrt{(R^3)/(GM)}`

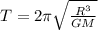
Where G is the gravitational constant and M is the mass of the sun.

`\begin{gathered} G=6.67*10^(-11)\text{ m}^3\text{kg}^(-1)\text{s}^(-2)\text{ } \\ M=2*10^(30)\text{ kg} \end{gathered}`

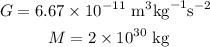
On substituting the known values in the equation of the orbital period,

`\begin{gathered} T=2\pi\sqrt{((6*10^(11))^3)/(6.67*10^(-11)*2*10^(30))} \\ =2.52*10^8\text{ s} \end{gathered}`

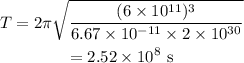
The circumference of the orbit of the asteroid is given by,

`c=2\pi R`

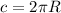
On substituting the known values,

`\begin{gathered} c=2\pi*6*10^(11) \\ =3.77*10^(12)\text{ m} \end{gathered}`

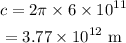
Thus the orbital speed of the asteroid is given by,

`v=(c)/(T)`

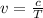
On substituting the known values,

`\begin{gathered} v=(3.77*10^(12))/(2.52*10^8) \\ =14.96*10^3\text{ m/s} \end{gathered}`

Final answer:

The orbital speed of the asteroid is 14.96×10³ m/s