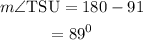Answer:
• x=7
,
• m∠TSU =89 degrees
Step-by-step explanation:
From the diagram:
Angles STU and TUS are opposite interior angles of angle TSW.
We know that 'the sum of the two opposite interior angles is equal to the exterior angle'.
Therefore:
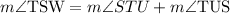
Substituting the given values, we have:
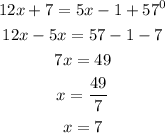
The value of x is 7.
Angles TSW and TSU are linear pairs. First, we find the value of TSW.
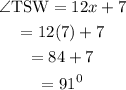
Therefore: