Question

Z2 =2−i,x2 =2,y2 =−1→r 2=5,sin(θ)=−1/5 →θ2=−26,z 2 /z 1 =(2.5) 0.5 (cos(−71)+isin(−71))

a) True
b) False

Answer 1

The given statement" z2 =2−i,x2 =2,y2 =−1→r 2=5,sin(θ)=−1/5 →θ2=−26,z 2 /z 1 =(2.5) 0.5 (cos(−71)+isin(−71)) is False.

Step-by-step explanation:

The expression

`\( (z_2)/(z_1) = (2.5)^(0.5) \cdot (\cos(-71) + i\sin(-71)) \)`

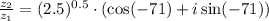
involves complex numbers. To assess its truth, let's break down the components. Firstly,
`\( z_2 \)` is represented as ( 2 - i), and
`\( z_1 \)` is given as ( 2). Now, ( r²) is calculated as ( x² + y²), yielding ( r² = 5 ) when
`\( x_2 = 2 \)` and
`\( y_2 = -1 \)`. This implies that (r ) is the square root of 5. Next,
`\( \sin(\theta) \)` is given as ( -1/5 ), which suggests
`\( \theta_2 = -26 \)` degrees.

Now,
`\( (z_2)/(z_1) \)` involves the division of
`\( z_2 \)` by
`\( z_1 \)`. Substituting the values, we get

`\( (2 - i)/(2) \)`

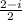
Simplifying this, we find

`\( (1 - (i)/(2)) \)`

The polar form of this complex number is

`\( (2.5)^(0.5) \cdot (\cos(-71) + i\sin(-71)) \)` .

However, on calculating, the polar form turns out to be
`\( (2.5)^(0.5) \cdot (\cos(109) + i\sin(109)) \)` , not
`\( (\cos(-71) + i\sin(-71)) \)` as given.

Therefore, the original statement is false.