1 Answer

JDiMatteo · Answer 1 · 2024-08-23T20:05:45+0000

the width of the 95% confidence interval for the mean length is approximately 3.492. So, the correct answer is: b) 3.492.

To find the width of the 95% confidence interval for the mean length, you can use the formula:

$\text{Width} = Z * \left( (s)/(√(n)) \right)$

where:

Z is the Z-score corresponding to the desired confidence level (for 95% confidence interval,
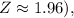
$$ Z \approx 1.96 $),$

s is the sample standard deviation, and

n is the sample size.

Let's calculate it:

1. **Calculate the sample mean
$($ \bar{x} $)$ :**

$\bar{x} = (62 + 59 + 57 + 60 + 61 + 58 + 63 + 56 + 57 + 57 + 60)/(11)$

2. **Calculate the sample standard deviation s:**

$s = \sqrt{\frac{\sum_(i=1)^(n)(x_i - \bar{x})^2}{n-1}}$

3. **Calculate the Z-score for 95% confidence interval
$($ Z \approx 1.96 $)$ :**

Now, substitute these values into the formula to find the width of the 95% confidence interval.

Let's perform the calculations.

1. **Calculate the sample mean
$($ \bar{x} $)$ :**

$\bar{x} = (62 + 59 + 57 + 60 + 61 + 58 + 63 + 56 + 57 + 57 + 60)/(11) \]\[ \bar{x} \approx 58.909$

2. **Calculate the sample standard deviation s:**

$s = \sqrt{\frac{\sum_(i=1)^(n)(x_i - \bar{x})^2}{n-1}} \]\[ s \approx 2.211$

3. **Calculate the Z-score for 95% confidence interval
$($ Z \approx 1.96 $):**\[ Z \approx 1.96 \]$

Now, plug these values into the formula:

$\text{Width} = 1.96 * \left( (2.211)/(√(11)) \right) \]\[ \text{Width} \approx 3.492$

Therefore, the width of the 95% confidence interval for the mean length is approximately 3.492. So, the correct answer is: b) 3.492.

Please log in or register to add a comment.